2021. 9. 21. 14:35ㆍ데이터/데이터 마이닝
머신러닝은 대표적으로 두가지 Supervised learning과 Unsupervised learning으로 나뉜다.
Supervised learning(지도 학습)
- 결과값이 이미 label 되어있는 경우 input값으로 output값을 예측
- Classfication, Regression(Numerical) 이 이에 속함.
Classfication - 스팸메일 여부판단, 고양이 사진으로 고양이인지 아닌지 판별하는 것
Regression - 주택가격 예측 , 온도에 따른 아이스크림 판매량 예측
Unsupervised learning(비지도 학습)
- 결과값이 label 되어있지 않고 input값들을 통해서 결과값을 해석하거나 그룹화 하는 것
- Clustering , Dimension Reduction, Association Rule Mining이 이에 속함
Clustering - 고객의 나이, 소득수준 등의 정보를 활용해 군집화 하는 것 (고객 세분화)
Dimension Reduction
Association Rule Mining(ex) - 두유를 장바구니에 담은사람이 기저귀도 많이 담더라 - > pattern의 발견
이번 글은 Supervised Learning의 선형회귀분석(Linear Regression)에 대해서 다룬다.
선형 회귀 분석(Linear Regression)
https://www.kaggle.com/ashydv/advertising-dataset
Advertising Dataset
www.kaggle.com
kaggle의 advertising매체와 sales에 관련된 데이터 셋을 가지고 선형회귀분석을 설명하려고 한다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
advertise = pd.read_csv('advertising.csv')
해당 데이터셋은 약 200개의 샘플로 TV, Radio, Newspaper, Sales라는 column들을 가지고 있다
plt.scatter(advertise['TV'],advertise['Sales'])
plt.xlabel("TV")
plt.ylabel("Sales")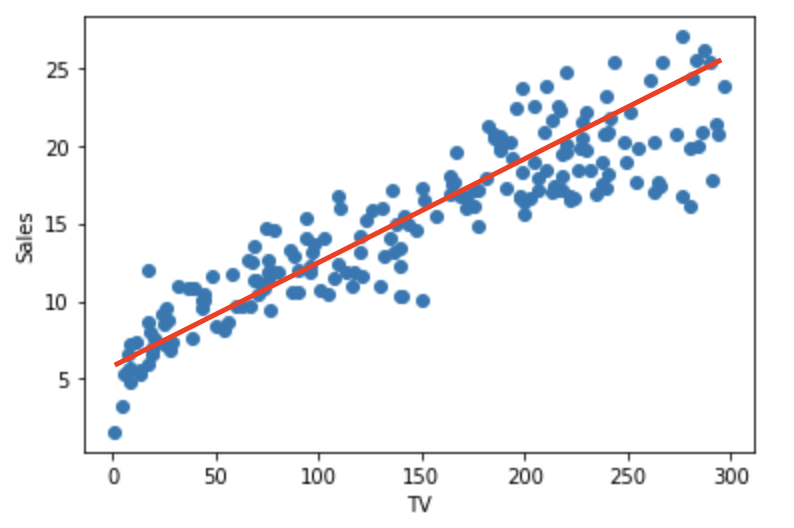
TV광고수에 따른 Sales의 값을 scatter plot으로 나타낸 것이고
빨간색 선은 임의로 그린 선그래프이다.
빨간색 선은 y = a*X + alpha 라는 함수로 x와 y의 관계식을 나타낼 수 있다. (Sales = A1 * TV + alpha)
다시말하면 선형회귀는 input변수들과 output변수의 관계로 위에있는 빨간색 선의 회귀식을 찾는것이다.
빨간색 선의 회귀식을 찾기위해서는 최소제곱법을 사용할수 있다.

첫번째 Sale식은 우리가 찾고자하는 회귀식이고
두번쨰 Sale은 우리가 가지고있는 실제데이터 값이다.
선형회귀분석의 4가지 가정
1. 선형성
2.오차의 등분산성
3.정규성
4.낮은 다중공산성
위의 데이터셋의 선형회귀분석 모델을 통해 4가지가정을 확인해보겠다.
1.선형성
-> 설명변수(input variable)각각 결과값(output variable)을 예측하는데 유의한지 아닌지 확인
개별 셜명변수들과 y값 사이 선형성을 확인하기위해 가설검정이 필요함.
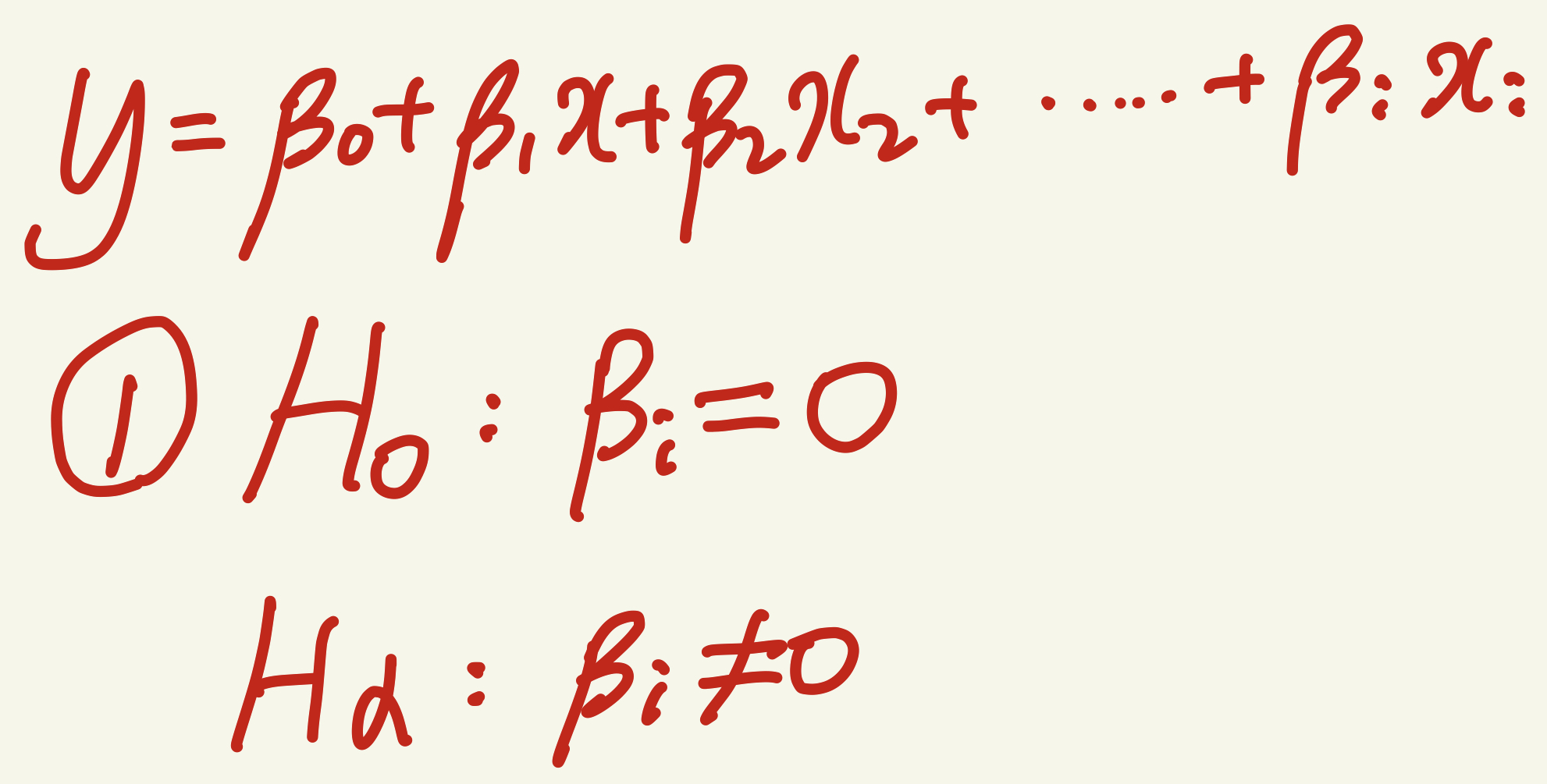
귀무가설 1번이 참이라면 (설명변수의 coefficient = 0이라면) y값과 설명변수간의 선형성(관계)이 존재하지 않으므로 해당설명변수는
모델에서 적합하지 않다.
이 가설검정 과정에서 T-test(평균의 차이가 유의미한지)를 사용하여 가설검정을 진행한다.
T-test는 통계파트에서 다루겠다.

Advertise 데이터 셋의 선형회귀 식을 위처럼 놓고 선형성 확인을 해보겠다.
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(advertise[['TV','Radio','Newspaper']],advertise['Sales'])
print("coefficient : " , reg.coef_)
print("intercept : " , reg.intercept_)결과값
coefficient : [0.05444578 0.10700123 0.00033566]
intercept : 4.625124078808655

위의 결과값들로 선형회귀식을 다음과 같이 세울수 있다

설명변수들 (Tv,Radio,Newspaper)의 T-test P-value값이 상당히 작으므로 귀무가설을 기각하고 대립가설을 채택한다
따라서 세개의 설명변수들 모두 Sales라는 목표값과 선형성을 이룬다고 할수있다
2.오차의 등분산성
오차의 등분산성 : 회귀선 기준으로 데이터들이 균등하게 분포되어야된다. -> 오차의 분산이 다르다면
즉, 예측값과 실제값사이 차이인 잔차의 분산과 실제값과 실제값들의 평균값과의 차이의 분산끼리 비교 분석을 분산분석(ANOVA)을 통해 차이가있는지 없는지 확인하기 위한 것이다.
3.오차의 정규성
Skewness값과 Kurtosis값을 활용한 Jarque - Bera Test를 통해서 오차가 정규분포를 따르는지 따르지 않는지 판단할 수 있다.

Jarque - Bera p-value 가 0.05 보다 크므로 Jarque-Bera검정의 귀무가설을 채택하여 이 모델의 오차는 정규성을 따른다고 판단할 수 있다.
또한
4.낮은 다중공산성
다중공산성을 다루기전에 먼저 Goodness of Fit에 대해 다루겠다.
Goodness of Fit이란 모형의 적합도(decide model's significance)를 양적으로 판단하기위한 것이다.
즉 선형회귀분석에서 모델 자체가 y값의 변화량을 설명하는데 유의한지 아닌지를 설명하는 것이다.
회귀분석에서는 Goodness of Fit을 R^2 으로 측정한다.
R^2을 이해하기위해선 위의 밑의 ANOVA TABLE에서 나올 SST = SSR + SSE에 대한 이해가 필요하다.

SST = SSR + SSE
R-squared = SSR/SST
-> R-squared값이 크다 -> 전체 Variance(fixed)된 값과 SSR-예측된값과 실제평균사이 variance가 비슷하다는 뜻 -> 다시말하면 SSE가 작다는것 -> Error가 작음 --> Linear Regression모델이 y값 의 variance 설명하는데 유의하다고 말할수 있다.
그래서 Linear Regression은 모델의 유의성 판단하는데 R^2과 Adujsted-R^2을 사용한다.
낮은 다중공산성이란 설명변수끼리의 관계(선형성)이 낮다는 것으로 다시말하면 설명변수끼리 서로 값에 영향을 주지않아야 된다는 것이다.
예를들면 위에 모델에서 TV광고가 증가하고 Radio광고가 낮아진다면 Newspaper광고가 커지는 서로 값에 크게 영향을 주면 다중공산성이 높으므로 Newspaper라는 설명변수는 다중공산성이 높아 설명변수로써 부적절할 수 있다는 것이다.
다중공산성을 체크하기위해서 분산팽창인수 (VIF : Variance Inflation Factor) 를 활용한다

1번식 선형회귀식에서의 설명변수들간의 선형관계를 확인하기위해 2번과같은 설명변수간의 선형회귀식을 만들어 VIF(j)를 구한다.
2번같은 과정은 모든 설명변수에대해서 진행해야하며 VIF를 구햇을때 값이 10이상이면 다중공산성이 크다고 판단하고 10보다 낮다면
인정할만한 다중공산성이라고 한다.
from statsmodels.stats.outliers_influence import variance_inflation_factor
from patsy import dmatrices
y, X = dmatrices('Sales ~TV+Radio+Newspaper', advertise, return_type = 'dataframe')
vif = pd.DataFrame()
vif["vif value"] = [variance_inflation_factor(X.values,i) for i in range(4)]
vif["explanatory variables"] = X.columns
vif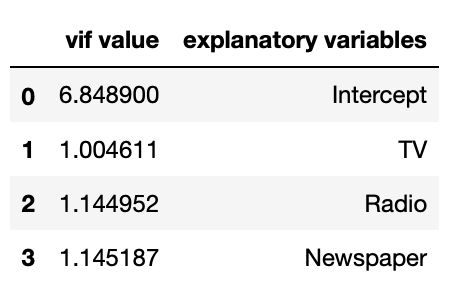
위의 선형회귀모델에서 구한 VIF값들이다 모두 10보다 작고 t-test도 통과하엿으므로 해당모델의 설명변수로 사용하기에 적절하다고 판단할 수있다.
F-test를 통한 모델의 유의성
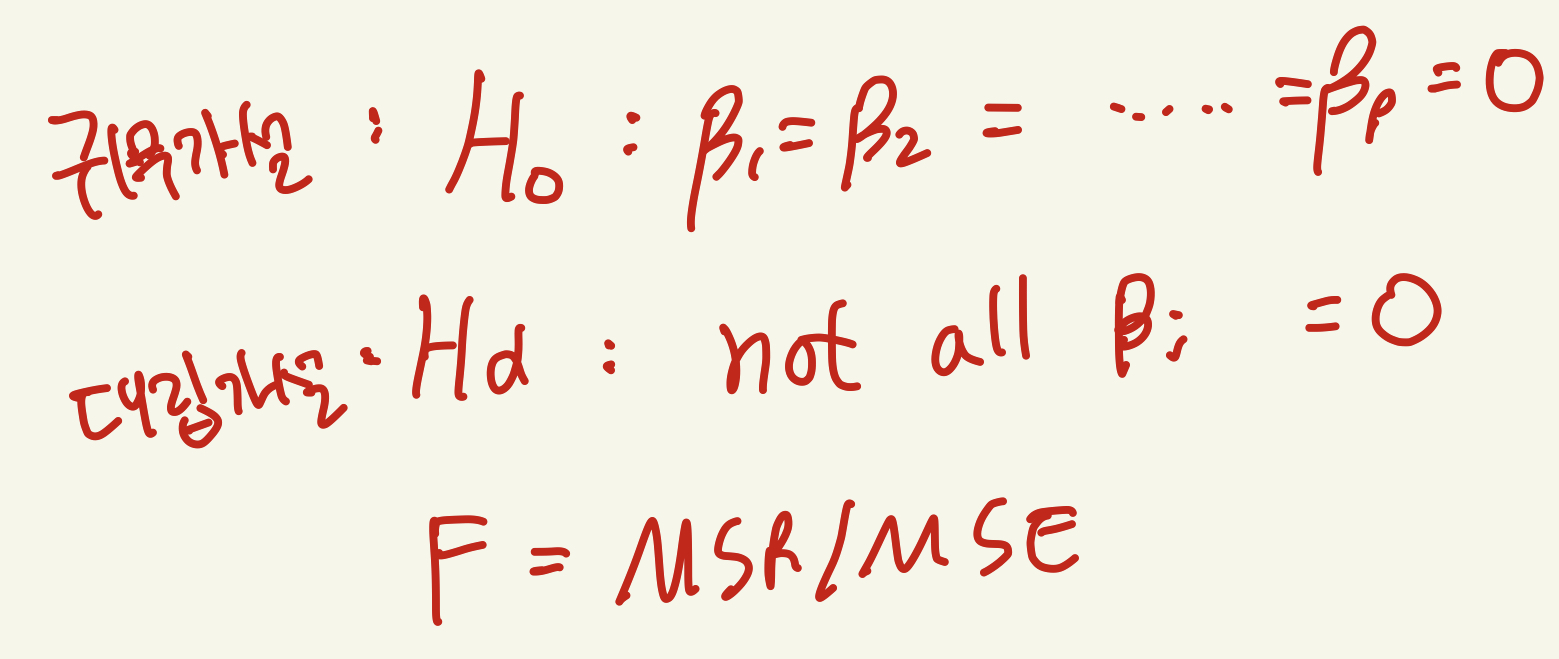
귀무가설은 회귀식의 coefficient들이 모두 0이라는 것이고 이것은 해당 모델이 목표값(target value)를 설명하는데 유의하지 않다는 것이다. 이는 이 모델이 target value 예측하는데 아무 쓸모 없다는 뜻이다.
따라서 F-test의 p-value가 높다면 해당모델은 유의하지 않다는 뜻이다.
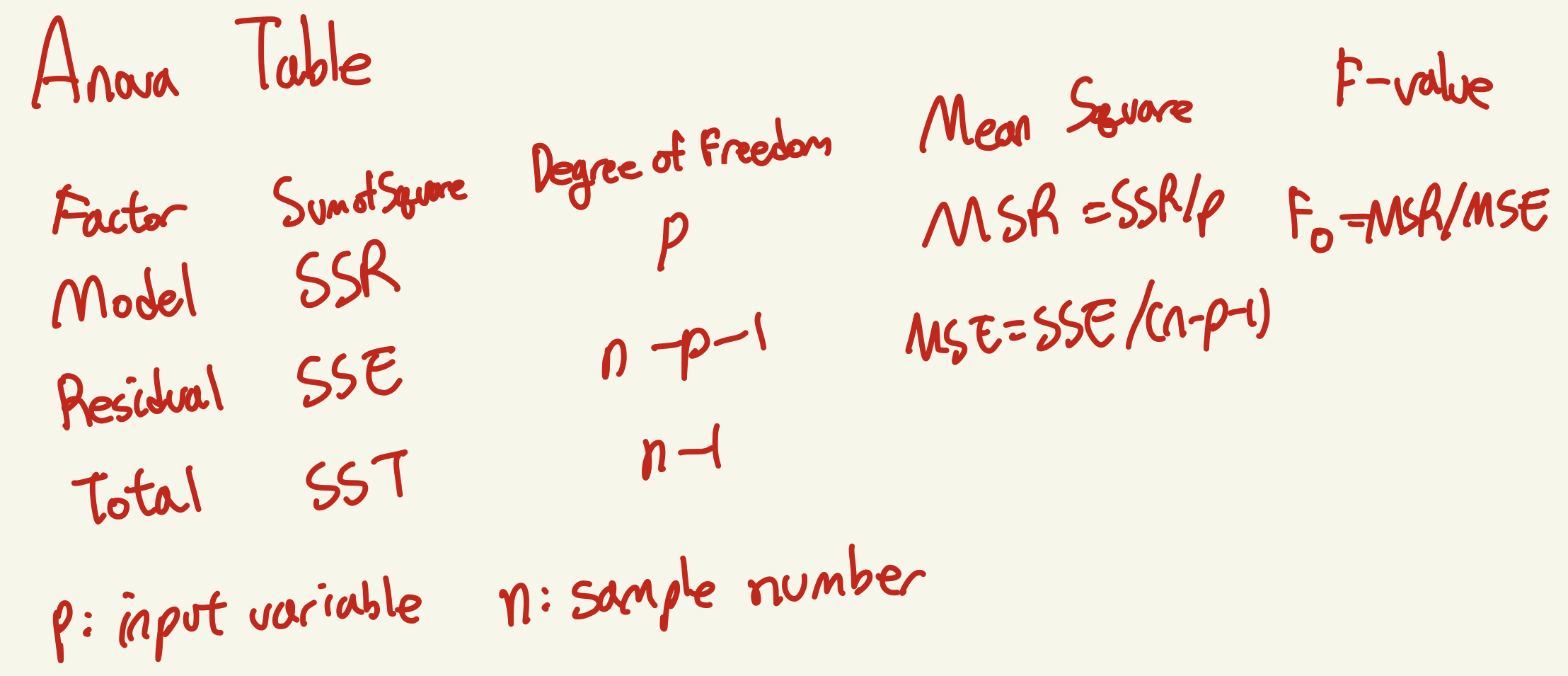
from scipy.stats import t,f,chi2,skew,kurtosis
y_true = advertise['Sales'].values
y_pred = reg.predict(advertise[['TV','Radio','Newspaper']])
SST = sum((y_true - np.mean(y_true))**2)
SSE = sum((y_true - y_pred)**2)
SSR = sum((y_pred - np.mean(y_true))**2)
n,p = advertise[['TV','Radio','Newspaper']].shape
MSE = SSE/(n-p-1)
MSR = SSR/p
f_value = MSR/MSE
pvalue = 1 - f.cdf(f_value,p,n-p-1)
print("------------------------------Anova Table-----------------------------------")
print("SSE :" , SSE , "\nP : " , p, "\nMSR : ", MSR ,"\nf :" ,f_value ,"\npvalue :", pvalue)
print("SSR :" , SSR, "\nn-p-1 :", (n-p-1), '\nMSE :', MSE)
print("SST :" , SST, "\nn-1 :", (n-1))------------------------------Anova Table-----------------------------------
SSE : 541.2012295254631
P : 3
MSR : 1671.5942401581808
f : 605.3801307108608
pvalue : 1.1102230246251565e-16
SSR : 5014.782720474543
n-p-1 : 196
MSE : 2.761230762885016
SST : 5555.983949999996
n-1 : 199
위의 코드 실행 결과값이다.
해당 모델의 F-test p-value가 0보다작으므로 귀무가설 기각하고 대립가설을 선택하므로 모든 coefficient의 값이 0이 아니므로 해당모델이 target value를 예측하는데 유의하다고 할 수 있다.
결론
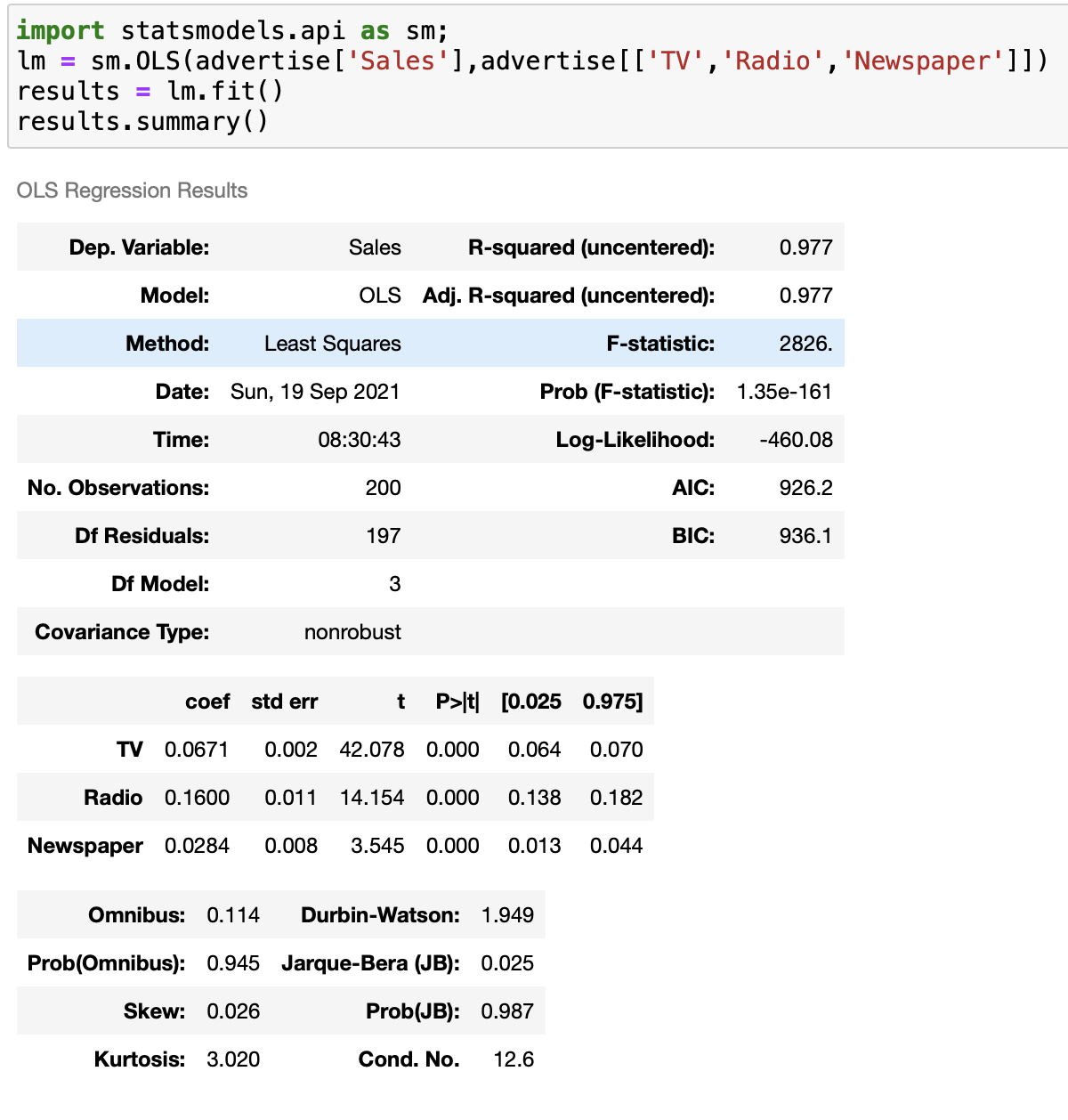
OLS (Ordinary Least Square) 모델을 통해 Regression한 모델의 결과이다

위의식은 위의 모델의 선형회귀식이며
이 모델은 선형회귀의 4가지 가정들 모두 만족시키며
TV, Radio, Newspaper 변수들은 모두 판매량과 양의 상관관계를 가지고 있으므로 TV,Radio,Newspaper광고들을 증가시키면 판매량이 증가할것이다. 또한 이모델에서 가장 큰 coefficient를 가진 Radio의 광고효과가 가장크다고 볼수도 있다.